Scoring
All scoring functions used in the CrowdCent Challenge can be found in the crowdcent_challenge.scoring module.
Symmetric NDCG@k
One of the key metrics used in some challenges is Symmetric Normalized Discounted Cumulative Gain (Symmetric NDCG@k).
Concept
Normalized Discounted Cumulative Gain (NDCG@k) is a metric used to evaluate how well a model ranks items. It assesses the quality of the top k predictions by:
- Giving higher scores for ranking truly relevant items higher.
- Applying a logarithmic discount to items ranked lower (meaning relevance at rank 1 is more important than relevance at rank 10).
- Normalizing the score by the best possible ranking (IDCG) to get a value between 0 and 1.
However, this commonly used metric only focuses on the top items in a list. In finance, identifying the worst performers (lowest true values) can be just as important as identifying the best.
Our metric of Symmetric NDCG@k addresses this by evaluating ranking performance at both ends of the list:
- Top Performance: It calculates the standard
NDCG@kbased on your predicted scores (y_pred) compared to the actual true values (y_true). This measures how well you identify the items with the highest true values. - Bottom Performance: It calculates another
NDCG@kfocused on the lowest ranks. It does this by:- Inverting both true values and predictions using
1 - valuetransformation - This makes originally low values (close to 0) become high values (close to 1), so standard NDCG rewards finding the originally lowest items
- Calculating
NDCG@kfor how well your lowest predictions match the items with the lowest true values
- Inverting both true values and predictions using
- Averaging: The final
symmetric_ndcg_at_kscore is the simple average of the Top NDCG@k and the Bottom NDCG@k.(NDCG_top + NDCG_bottom) / 2.
Calculation
The Symmetric NDCG@k is calculated as:
- Top NDCG@k: Calculate standard NDCG@k using true values and predicted scores
- Bottom NDCG@k: Invert both true values and predictions using
1 - value, then calculate NDCG@k - Final Score: Average of top and bottom NDCG@k scores:
(NDCG_top + NDCG_bottom) / 2
The standard NDCG formula includes:
- DCG@k = Σ(relevance_i / log₂(i+1)) for i=1 to k
- IDCG@k = DCG@k for ideal ranking
- NDCG@k = DCG@k / IDCG@k
Interpretation
Notably, Symmetric NDCG@k does not give 0.5 for random predictions, but ~0.55 for our default k=40. Understanding the random baseline is crucial for interpreting your scores.
- NDCG@k = 1: perfect performance at identifying both the top k best and bottom k worst items according to their true values.
- NDCG@k = 0.55: random guessing.
- NDCG@k = 0: no overlap with top k or bottom k.
How k Affects the Random Baseline:
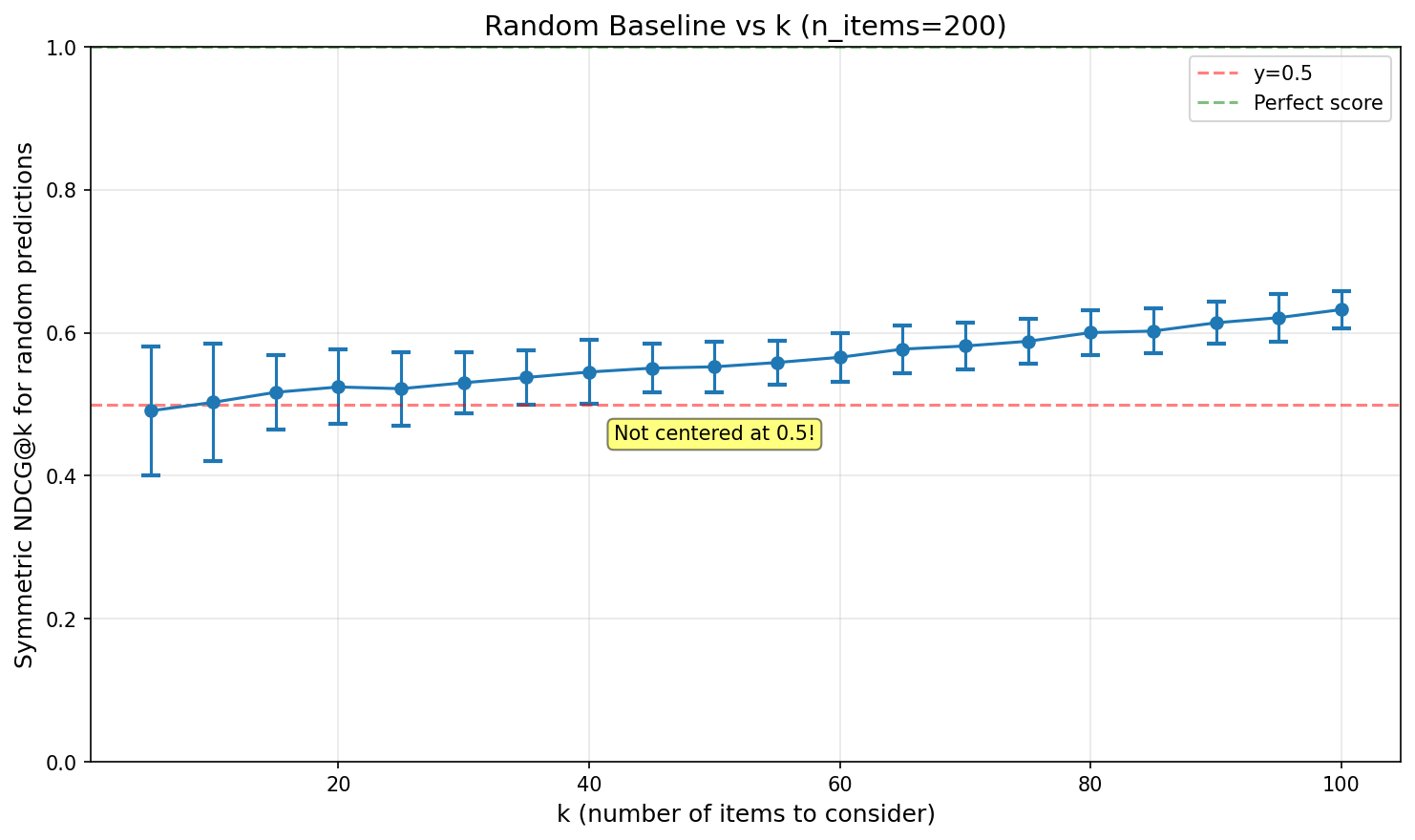
Key insights:
- Random baseline starts near 0.5 for small k and increases monotonically
- For Hyperliquid (k=40, n≈170-200), random predictions score ~0.55
Usage
from crowdcent_challenge.scoring import symmetric_ndcg_at_k
import numpy as np
# Example data
y_true = np.array([0.1, 0.2, 0.9, 0.3, 0.7])
y_pred = np.array([0.2, 0.1, 0.8, 0.4, 0.6])
k = 3
score = symmetric_ndcg_at_k(y_true, y_pred, k)
This metric provides a more holistic view of ranking performance when both high and low extremes are important.
Spearman Correlation
Spearman's rank correlation coefficient is a non-parametric measure of rank correlation that assesses how well the relationship between two variables can be described using a monotonic function.
Concept
In the context of ranking challenges, Spearman correlation measures how well your predicted rankings align with the true rankings. Unlike Pearson correlation (which measures linear relationships), Spearman correlation:
- Works with ranks: It converts both predicted and true values to ranks before computing correlation
- Captures monotonic relationships: Perfect Spearman correlation (±1) means perfect monotonic relationship, even if not linear
- Robust to outliers: Since it uses ranks rather than raw values, extreme values have less influence
Calculation
The Spearman correlation coefficient (ρ) is calculated as:
- First, convert both
y_trueandy_predto ranks - Then calculate the Pearson correlation coefficient on these ranks
- Formula: ρ = 1 - (6 × Σd²) / (n × (n² - 1)), where d is the difference between paired ranks
Interpretation
- ρ = 1: Perfect positive correlation (your rankings perfectly match the true rankings)
- ρ = 0: No correlation (your rankings are unrelated to the true rankings)
- ρ = -1: Perfect negative correlation (your rankings are exactly reversed)
Usage
from scipy.stats import spearmanr
import numpy as np
# Example data
y_true = np.array([1.0, 0.5, 0.3, 0.2, 0.1]) # True values (will be ranked)
y_pred = np.array([0.9, 0.6, 0.25, 0.22, 0.05]) # Predicted values (will be ranked)
# Calculate Spearman correlation
correlation, p_value = spearmanr(y_true, y_pred)